Activation functions

Why we need?

• add non-linear factor, solve the problem that linear models cannot represent
• Provide better interpretability to the model

Common activations

Sigmoid

\[sig(z) = \frac{1}{e^{-z} + 1}\] \[sig'(z) = sig(z)(1 - sig(z))\]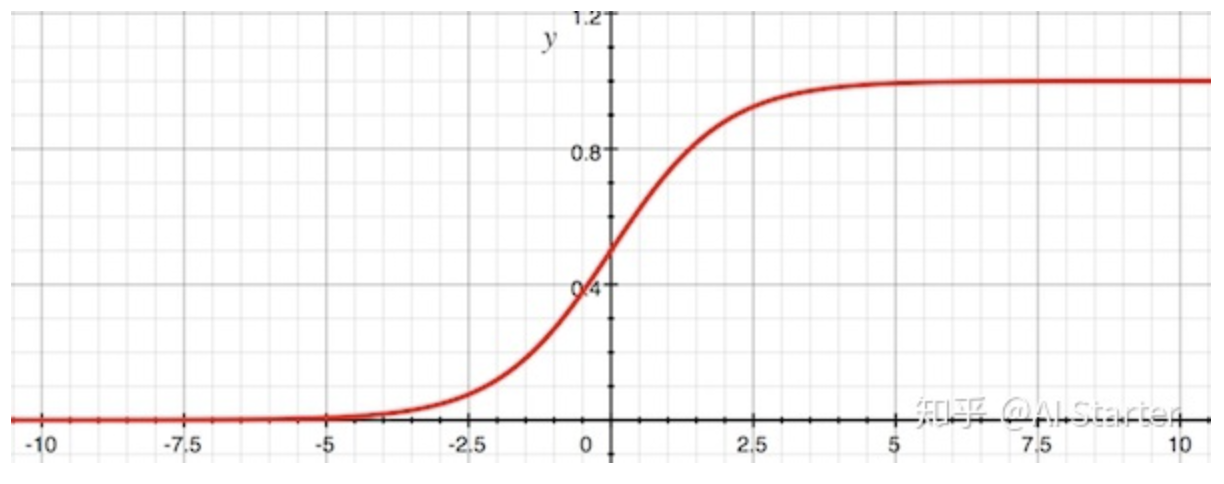

• cons
  • left and right all saturated, gradient vanishing
  • exponential computation
  • not zero-centered, lower convergence speed

tanh

\[tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]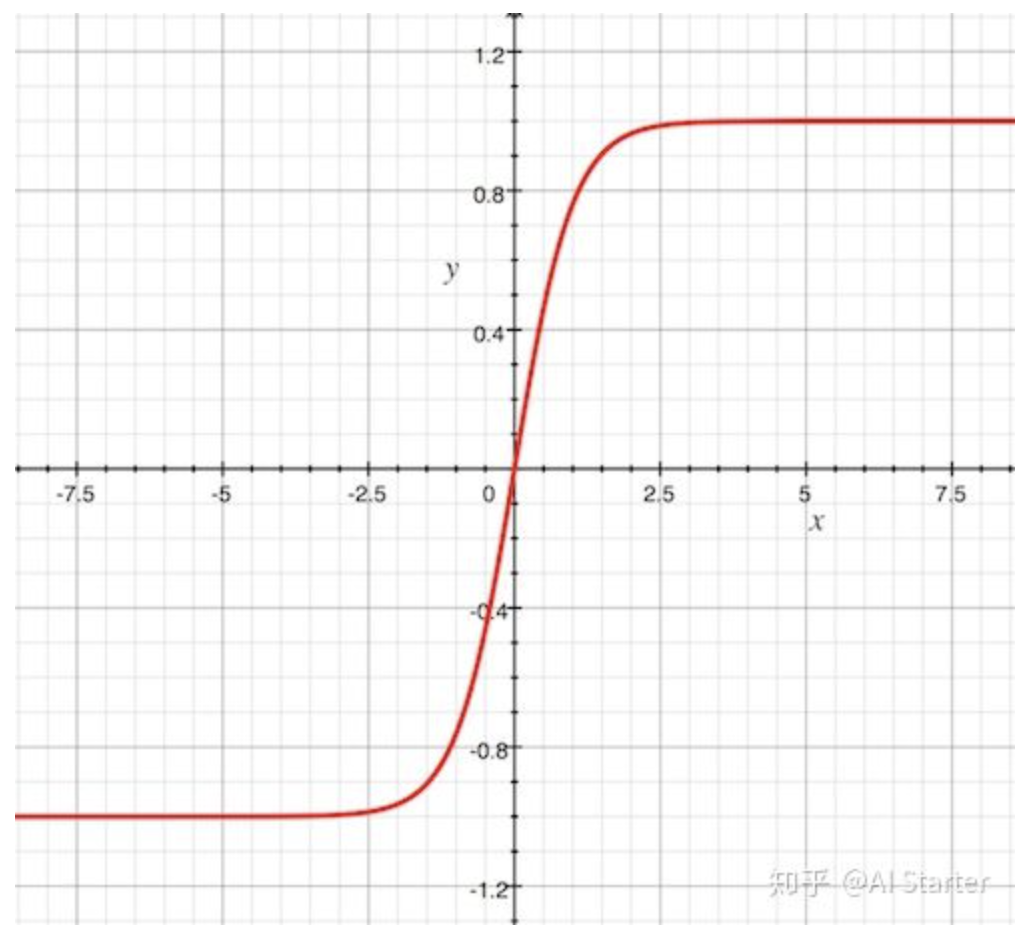

range from (-1, 1)

adv:

• compared with sigmoid
  • faster convergence speed, larger slope near 0
  • output mean 0
  • larger saturated space

Softmax

\[softmax(z) = \frac{e^{z_i}}{\sum_{j=1}^{K}e^{z_j}}\]

relu

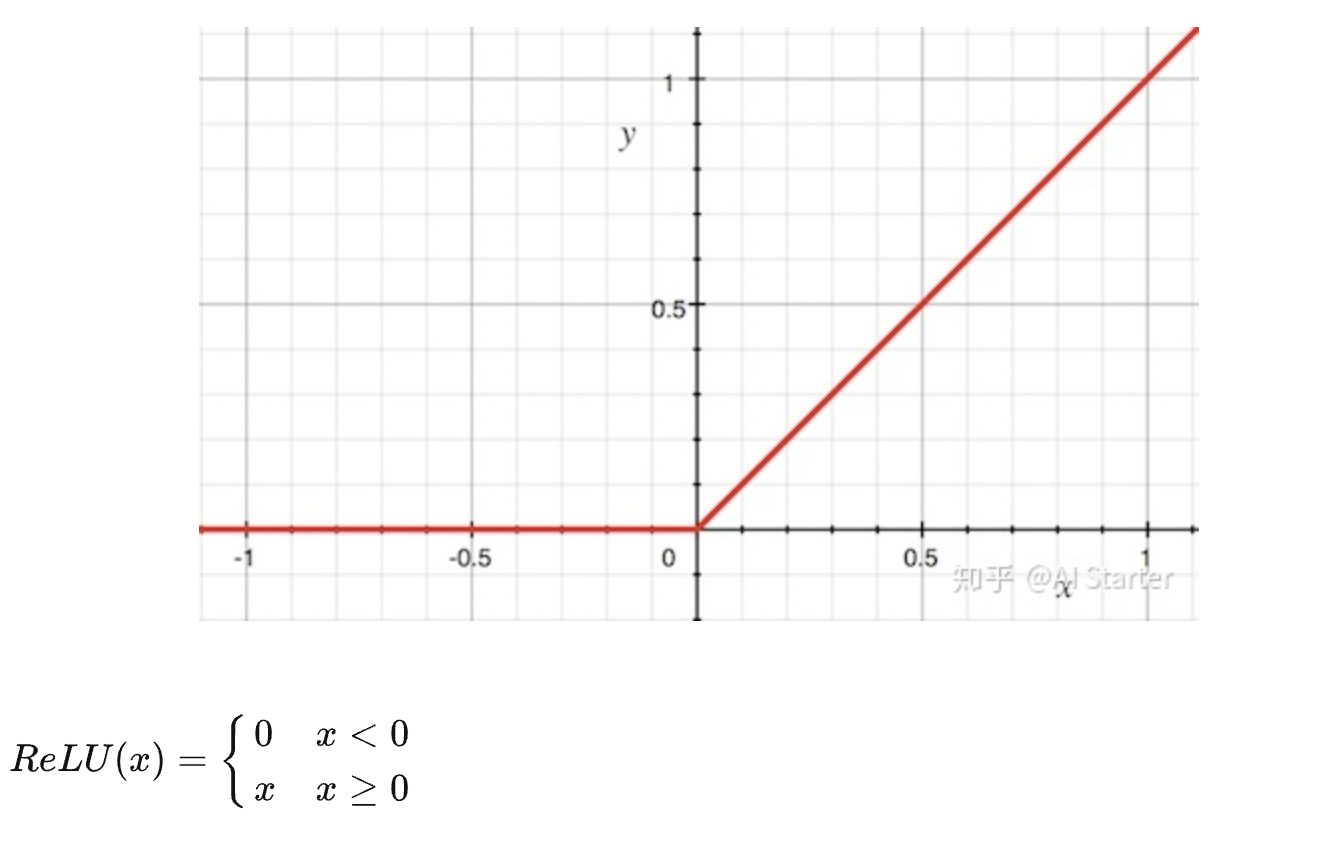
dead relu problem: when $ x < 0 $ , ReLU output 0, when backpropagation, the gradient always 0, parameter will never be updated.

• adv:
  • easy computation
  • more similar to bio-inspired mechanism compared to tanh, sigmoid
  • does not saturate, solve vanishing gradient
  • fast convergence
• cons:
  • not zero centered
  • dead relu problem

leaky relu

\[LeakyReLU(x) = max(0.01x, x)\]

adv:

• no dead relu problem

elu

\[ELU(x) = x, x > 0\\ ELU(x) = \alpha(e^x - 1), x \leq 0\]

• adv
  • mean activation close to 0
  • more robust to noise
• con
  • exponential computation

maxout

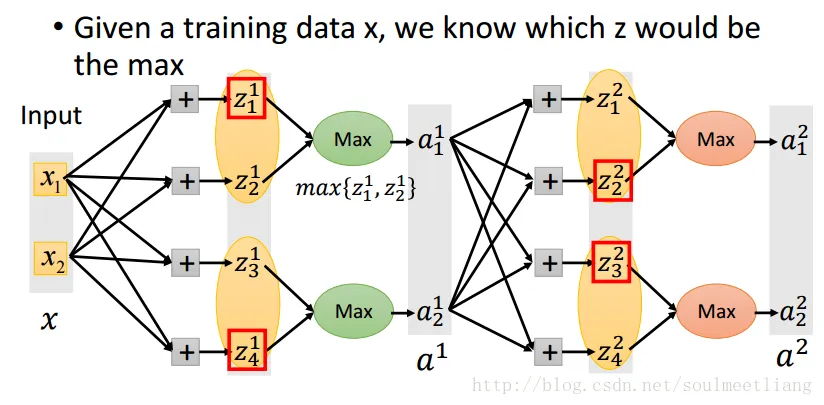
It is a learnable activation function

• Activation function in maxout network can be any piece-wise linear convex function
• How many pieces depending on how many elements in a group

---